如今的車輛采用獨立鉸鏈轉向,這令阿克曼角成為一個重要但又無法充分實現的參數,。這是由于獨立鉸鏈轉向方式也會破壞轉向穩(wěn)定性,,當把轉向時所有輪軸的延長線進行相交,,尋找車輛瞬態(tài)轉向中心時,,問題會暴露得十分明顯,。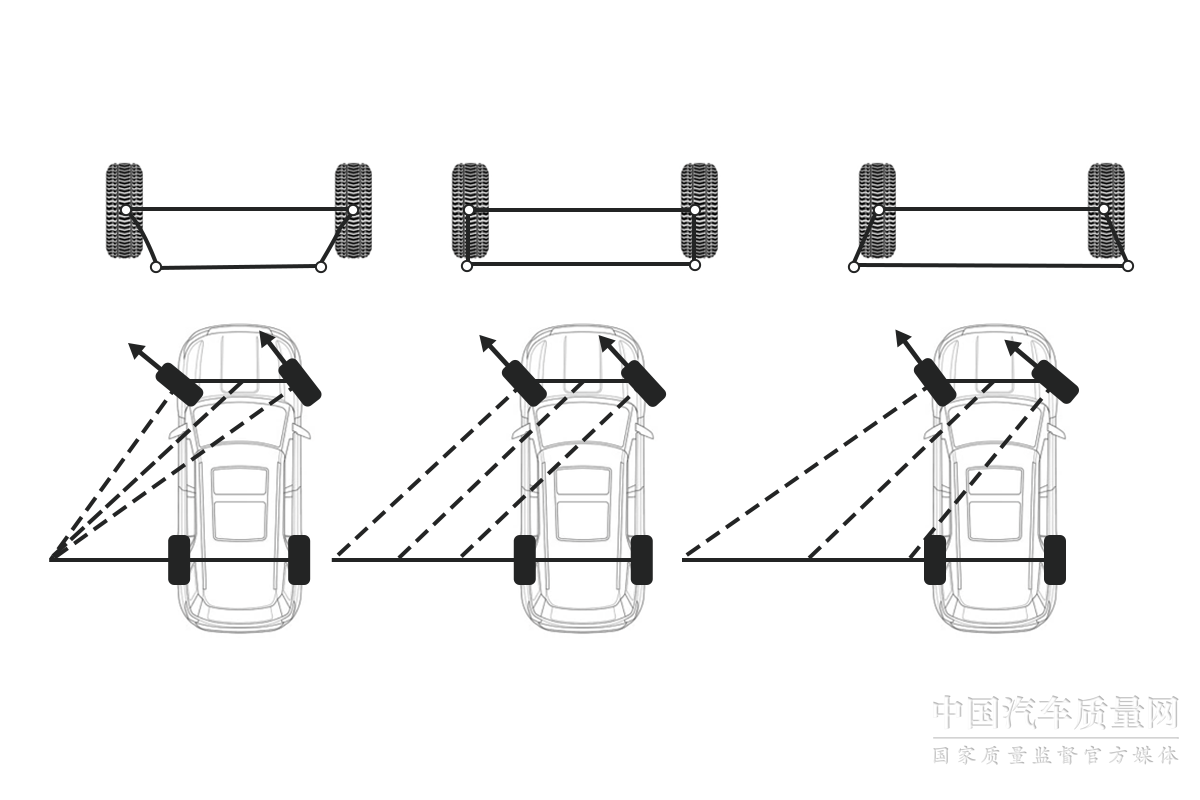
由于導向輪擁有相同轉向角之后,,輪軸延長線之間形成的是平行線,,并不相交,,所以無法產生交點,,兩個導向輪各轉各的,輪胎會出現滑動甚至彈跳的情況,。
由此,,便需要內側的導向輪轉向角更大,外側導向輪轉向角更小,,讓所有輪軸延長線獲得共同交點,。此時兩個導向輪輪軸延長線之間的夾角,便是大家熟悉又陌生的“阿克曼角”,。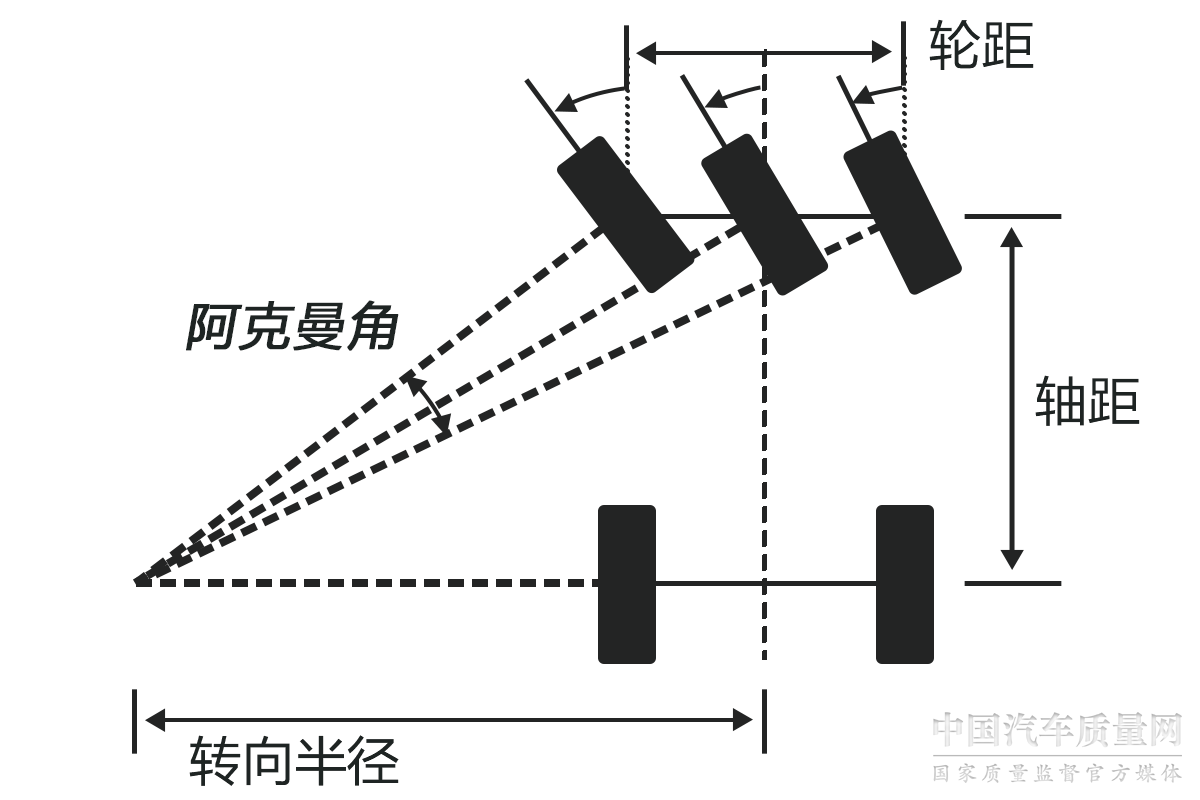
想要獲得阿克曼角可以通過軸距,、輪距和轉彎半徑獲得。首先,,將車輪數量簡化,,取各軸兩輪之間的中點,將四輪簡化為二輪,,連接二者的輪軸延長線就能得到一個理想的瞬態(tài)轉向中心,,以及轉向半徑。
此時,,我們再將剩余輪軸與瞬態(tài)轉向中心相連,,就得到兩個導向輪輪軸之間的夾角關系。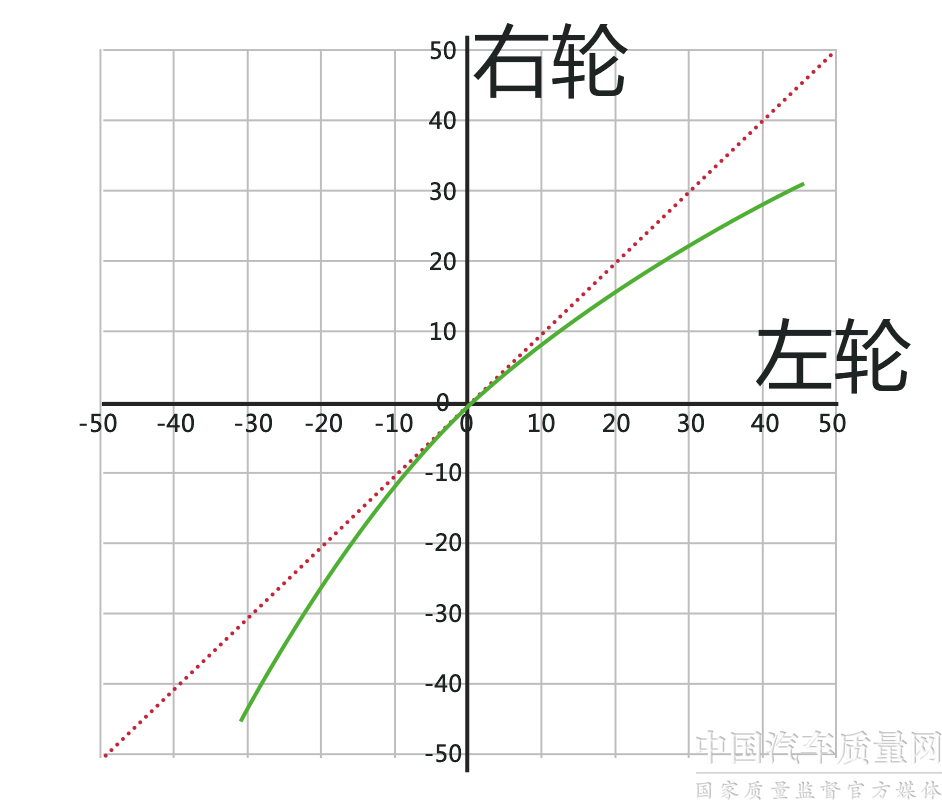
(綠線:阿克曼角轉向曲線)
這個夾角關系是在瞬態(tài)轉向中心參數計算下的結果,而車輛是時刻運動變化的,,因此轉向角度是一個范圍并非固定數值,。不同轉向角度下,阿克曼角數值不斷變化,,整個范圍內兩導向輪輪軸之間的夾角關系如上表所示,。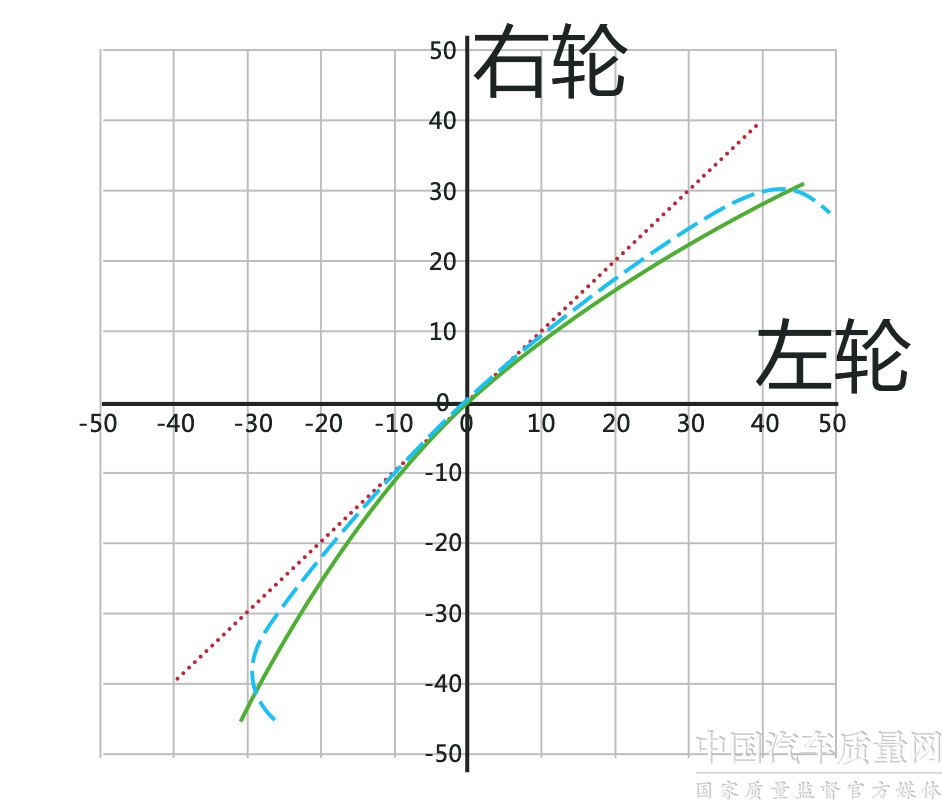
(藍色虛線:加入轉向梯形后導向輪輪軸夾角曲線)
這種曲線特性使每個轉向角度都達成100%的阿克曼角成為一種十分復雜的事情,意味著兩個車輪都需要獨立的控制器,,根據不同轉向角進行控制,。這還不是問題的關鍵,車輛運動中復雜的力學變化會施加在輪胎,、連桿,、懸架車身等位置,造成不同程度的形變,,這令計算阿克曼角的每一個數值都是變量,,使計算復雜程度呈幾何級上升。
那么,,當下車輛是如何滿足阿克曼角條件的呢,?
答案是——轉向梯形。在這個平面四桿機構中,,如果轉向橫拉桿作為短邊且位于輪軸后方,,則使內側車輪的轉動速率更快。反之,,如果轉向橫拉桿變?yōu)殚L邊則需要在輪軸之前實現相同效果,,使兩個導向輪變化夾角的曲線更加趨近于阿克曼角曲線。
這仍然不能解決所有問題,,所以在實際車輛設計過程中,,不會完全按照阿克曼角進行轉向幾何設計,而是根據不同的車輛設計取向,、懸架形式,,針對性計算,在賽車或者部分運動取向的車型上甚至會看到反阿克曼角,,即內側轉向角小外側轉向角大,。
(資料來源:《汽車設計》)

